How To Make A Floor Function Equal A Ceiling

The int function short for integer is like the floor function but some calculators and computer programs show different results when given negative numbers. 0 x. In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or.

is canned light tuna cooked internal pivot door systems iron fence installation birmingham al how to kill mold in basement floor irish wedding rings claddagh how to get supply crate keys in killing floor 2 irobot wall barrier how to make a sewing machine mat with pockets

The Floor Function And The Ceiling Function Maple Programming Help

How To Use The Excel Ceiling Function Exceljet

Framing A Tray Ceiling Google Search Tray Ceiling Ceiling Design Ceiling Design Modern

Rounding In R 4 Examples Round Ceiling Floor Trunc Signif Functions

Mixed Equal Parts Special Walnut Espresso And Provincial In The Minwax Brand For Our Stain 1 Part Sp Floor Stain Colors Staining Wood Wood Floor Stain Colors

Ceiling In A Sorted Array Geeksforgeeks

The best strategy is to break up the interval of integration or summation into pieces on which the floor function is constant.

How to make a floor function equal a ceiling.

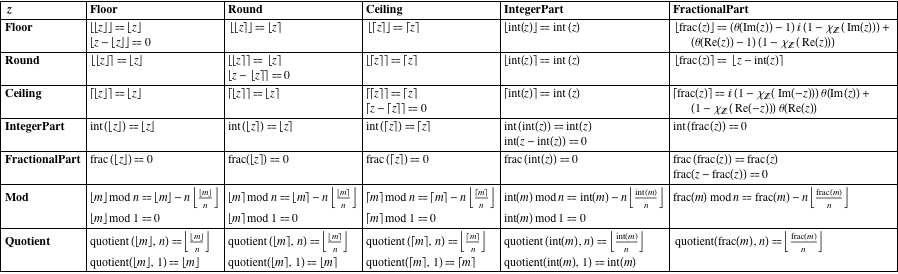
The least integer that is greater than or equal to x as a graph the floor function is this curious step function like an infinite staircase. Since x x x was chosen arbitrarily we have x 1 x x 1 lfloor x rfloor x 1 x for all x x x. But then n n n cannot be the greatest integer less than or equal to x x x so we have a contradiction. Evaluate 0 x e x d x.

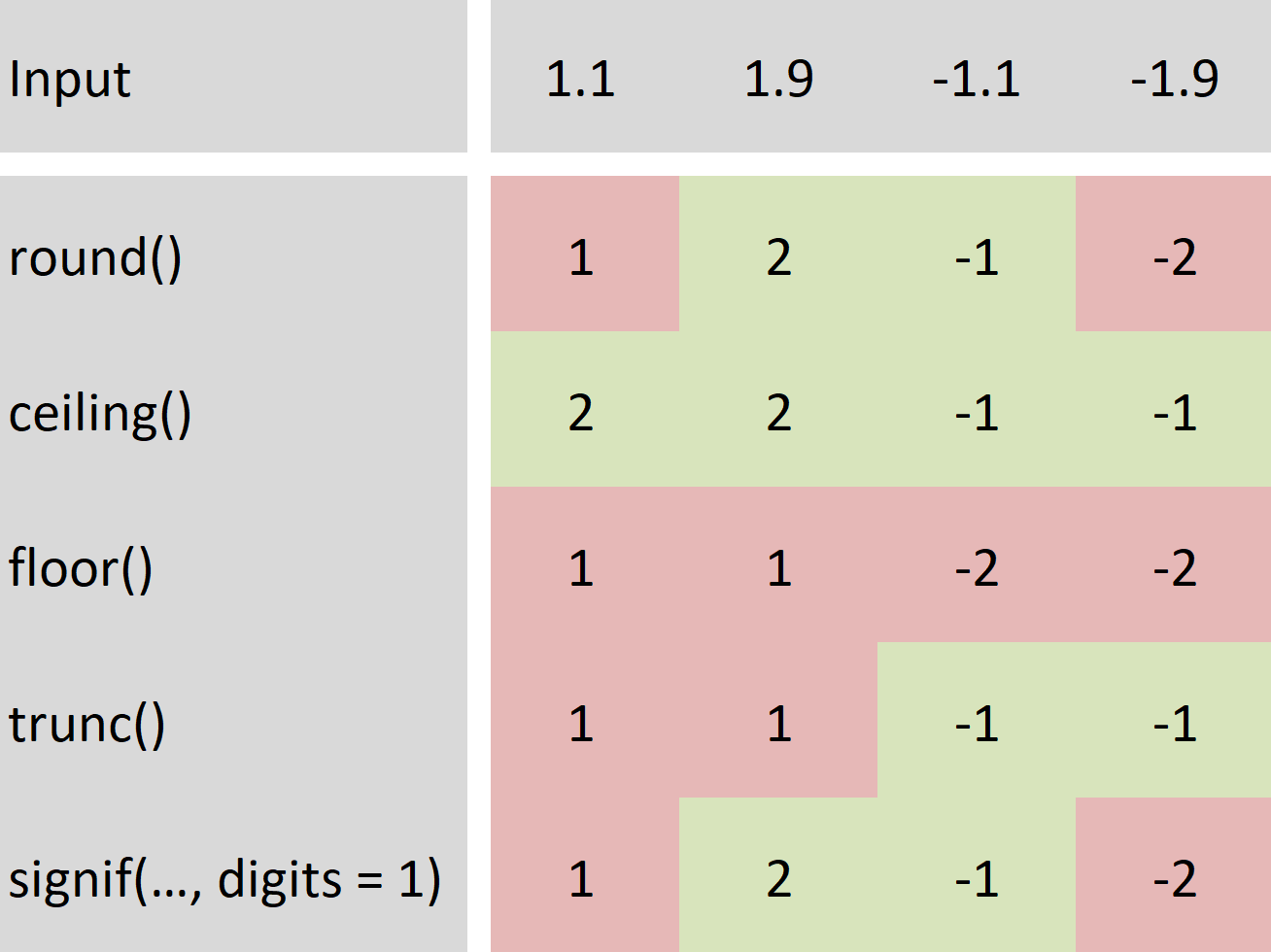
Similar considerations can be made for the ceil function lceil cdot rceil and we get the. So the ceiling function rounds a number up the floor function rounds a number down. Definite integrals and sums involving the floor function are quite common in problems and applications. For example and while.

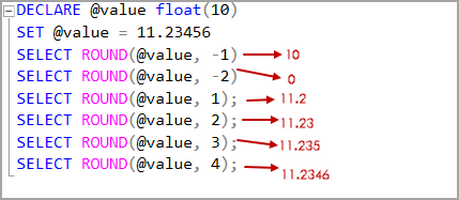
Some say int 3 65 4 the same as the floor function. A floor function takes a real number x and sends it to the greatest integer less than or equal to x. Int limits 0 infty lfloor x rfloor e x dx. And this is the ceiling function.

How To Operate With Floor And Ceiling Functions

Soundproofing Material Acoustic Panels Soundproof Foam Exposed Basement Ceiling Low Ceiling Basement Exposed Ceilings

Pin By Martis Siregar On Basement Reno In 2020 Basement Ceiling Basement Apartment Basement Remodeling

Overview Of Sql Server Rounding Functions Sql Round Ceiling And Floor

Rounding

A Summer House In The Countryside Of Bohemia Czech Republic Summer House Gable Roof House House Roof

Floor To Ceiling Log Firewood Storage Beside A Fireplace If You Re Out Of Logs By Summer You Can Use The Niche Living Room Photos Family Room Home Fireplace

The Floor Is Awesome But I M Not Sure I Can Say The Same Thing For The Ceiling Floor Design Architecture Flooring

How To Plan And Design A Shower Niche Room For Tuesday Shower Niche Bathrooms Remodel Marble Showers

How Cool Is This Metal Ceiling In The Basement Low Ceiling Basement Basement Ceiling Diy Basement

Floor Bricks Design Brick Flooring Brick Design Flooring

Galeria De Xanc I Meli Amoo 5 Diy Interior Doors Interior Design Courses Online Retro Interior

Ceiling Function Introduction To The Rounding And Congruence Functions

Equal Parts Function And Flair The Contemporary Chandelier Has Actually Come A Long Method F In 2020 Pendant Ceiling Lamp Iron Ceiling Lights Crystal Pendant Lighting

Industrial Office Flooring Jotterwood Vinyl Flooring Singapore Laminate Flooring Singapore Engine Vinyl Flooring Engineered Wood Floors Best Vinyl Flooring

Pin By De Carina Kamini On Dream Home Vaulted Ceiling Living Room Livingroom Layout Ceiling Lights Living Room

Checkered Solid Brass Floor Register Flooring One Level Homes Cast Iron

Plywood Garage Garage Interior Plywood Ceiling Plywood Walls

Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gctytky5u5byykbdpajijm0olfn 2bmit7pyar0av3q2flnx07sd Usqp Cau

Drop Ceiling Lighting Ideas Drop Ceiling Lighting Dropped Ceiling Ceiling Lights

Rustic Faux Timber Ceiling Beam Profile Jpg 480 310 Ceiling Beams Wood Beam Ceiling Faux Wood Beams

One Room Challenge Week 5 Diy Ceiling Makeover Diy Ceiling Beadboard Ceiling Coffered Ceiling

Gorgeous Locker For Each Family Member At The First Glance I Loved The Last Shot Stunning And Deeply Shocked By The Powerful Storage Functio Veranda Interiors

We Built This Home With Tall 10 4 Ceiling Height On The Main And Used Large Floor To Ceiling Wind Breakfast Table Living Room Windows Floor To Ceiling Windows

Source : pinterest.com